ฟังก์ชันกำลัง คุณสมบัติ และกราฟ ฟังก์ชั่นพลังงาน
เพื่อความสะดวกในการพิจารณาฟังก์ชันกำลัง เราจะพิจารณา 4 กรณีแยกกัน: ฟังก์ชันกำลังที่มีเลขชี้กำลังธรรมชาติ ฟังก์ชันกำลังที่มีเลขชี้กำลังจำนวนเต็ม ฟังก์ชันกำลังที่มีเลขชี้กำลังเป็นตรรกยะ และฟังก์ชันกำลังที่มีเลขชี้กำลังไม่ลงตัว
ฟังก์ชันยกกำลังพร้อมเลขชี้กำลังธรรมชาติ
ก่อนอื่น เรามาแนะนำแนวคิดของปริญญาที่มีเลขชี้กำลังตามธรรมชาติกันดีกว่า
คำจำกัดความ 1
กำลังของจำนวนจริง $a$ ที่มีเลขชี้กำลังธรรมชาติ $n$ คือตัวเลขที่เท่ากับผลคูณของตัวประกอบ $n$ ซึ่งแต่ละตัวจะเท่ากับตัวเลข $a$
ภาพที่ 1.
$a$ เป็นฐานของปริญญา
$n$ เป็นเลขชี้กำลัง
ตอนนี้ให้เราพิจารณาฟังก์ชันกำลังที่มีเลขชี้กำลังตามธรรมชาติ คุณสมบัติ และกราฟของมัน
คำจำกัดความ 2
$f\left(x\right)=x^n$ ($n\in N)$ เรียกว่าฟังก์ชันยกกำลังที่มีเลขชี้กำลังธรรมชาติ
เพื่อความสะดวกยิ่งขึ้น เราจะพิจารณาแยกฟังก์ชันยกกำลังที่มีเลขชี้กำลังเลขคู่ $f\left(x\right)=x^(2n)$ และฟังก์ชันยกกำลังที่มีเลขชี้กำลังคี่ $f\left(x\right)=x^ (2n-1)$ ($n\ใน N)$
คุณสมบัติของฟังก์ชันกำลังที่มีเลขชี้กำลังเลขคู่ตามธรรมชาติ
$f\left(-x\right)=((-x))^(2n)=x^(2n)=f(x)$ -- ฟังก์ชันเป็นเลขคู่
พื้นที่ค่า -- $\
ฟังก์ชันลดลงเป็น $x\in (-\infty ,0)$ และเพิ่มขึ้นเป็น $x\in (0,+\infty)$
$f("")\left(x\right)=(\left(2n\cdot x^(2n-1)\right))"=2n(2n-1)\cdot x^(2(n-1) ))\ge 0$
ฟังก์ชันนี้นูนออกมาตลอดขอบเขตคำจำกัดความ
พฤติกรรมที่ส่วนท้ายของโดเมน:
\[(\mathop(lim)_(x\to -\infty ) x^(2n)\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) x^( 2n)\ )=+\infty \]
กราฟ (รูปที่ 2)

รูปที่ 2 กราฟของฟังก์ชัน $f\left(x\right)=x^(2n)$
คุณสมบัติของฟังก์ชันยกกำลังที่มีเลขชี้กำลังคี่ตามธรรมชาติ
โดเมนของคำจำกัดความคือจำนวนจริงทั้งหมด
$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ -- ฟังก์ชันเป็นเลขคี่
$f(x)$ ต่อเนื่องตลอดโดเมนคำจำกัดความทั้งหมด
พิสัยเป็นจำนวนจริงทั้งหมด
$f"\left(x\right)=\left(x^(2n-1)\right)"=(2n-1)\cdot x^(2(n-1))\ge 0$
ฟังก์ชันนี้จะเพิ่มขึ้นทั่วทั้งขอบเขตคำจำกัดความ
$f\left(x\right)0$ สำหรับ $x\in (0,+\infty)$
$f(""\left(x\right))=(\left(\left(2n-1\right)\cdot x^(2\left(n-1\right))\right))"=2 \left(2n-1\right)(n-1)\cdot x^(2n-3)$
\ \
ฟังก์ชันนี้มีลักษณะเว้าสำหรับ $x\in (-\infty ,0)$ และนูนสำหรับ $x\in (0,+\infty)$
กราฟ (รูปที่ 3)
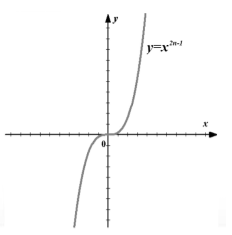
รูปที่ 3 กราฟของฟังก์ชัน $f\left(x\right)=x^(2n-1)$
ฟังก์ชันยกกำลังพร้อมเลขชี้กำลังจำนวนเต็ม
ก่อนอื่น เรามาแนะนำแนวคิดของปริญญาที่มีเลขชี้กำลังจำนวนเต็มกันก่อน
คำจำกัดความ 3
กำลังของจำนวนจริง $a$ ที่มีเลขชี้กำลังจำนวนเต็ม $n$ ถูกกำหนดโดยสูตร:

รูปที่ 4.
ให้เราพิจารณาฟังก์ชันยกกำลังที่มีเลขชี้กำลังจำนวนเต็ม คุณสมบัติ และกราฟของมัน
คำจำกัดความที่ 4
$f\left(x\right)=x^n$ ($n\in Z)$ เรียกว่าฟังก์ชันยกกำลังที่มีเลขชี้กำลังจำนวนเต็ม
ถ้าดีกรีมากกว่าศูนย์ เราก็มาถึงกรณีของฟังก์ชันกำลังที่มีเลขชี้กำลังธรรมชาติ เราได้พูดคุยกันแล้วข้างต้น สำหรับ $n=0$ เราจะได้ฟังก์ชันเชิงเส้น $y=1$ เราจะปล่อยให้ผู้อ่านพิจารณา ยังคงต้องพิจารณาคุณสมบัติของฟังก์ชันกำลังด้วยเลขชี้กำลังจำนวนเต็มลบ
คุณสมบัติของฟังก์ชันยกกำลังที่มีเลขชี้กำลังจำนวนเต็มลบ
โดเมนของคำจำกัดความคือ $\left(-\infty ,0\right)(0,+\infty)$
ถ้าเลขชี้กำลังเป็นคู่ ฟังก์ชันก็จะเป็นเลขคู่ ถ้าเป็นเลขคี่ แสดงว่าฟังก์ชันเป็นเลขคี่
$f(x)$ ต่อเนื่องตลอดโดเมนคำจำกัดความทั้งหมด
ขอบเขต:
ถ้าเลขชี้กำลังเป็นเลขคู่ แล้ว $(0,+\infty)$; ถ้าเป็นเลขคี่ แล้ว $\left(-\infty ,0\right)(0,+\infty)$
สำหรับเลขชี้กำลังคี่ ฟังก์ชันจะลดลงเป็น $x\in \left(-\infty ,0\right)(0,+\infty)$ ถ้าเลขชี้กำลังเป็นเลขคู่ ฟังก์ชันจะลดลงเป็น $x\in (0,+\infty)$ และเพิ่มขึ้นเป็น $x\in \left(-\infty ,0\right)$
$f(x)\ge 0$ ทั่วทั้งโดเมนของคำจำกัดความ
ให้ข้อมูลอ้างอิงเกี่ยวกับฟังก์ชันเลขชี้กำลัง - คุณสมบัติพื้นฐาน กราฟ และสูตร หัวข้อต่อไปนี้ได้รับการพิจารณา: โดเมนของคำจำกัดความ เซตของค่า ความซ้ำซ้อน ฟังก์ชันผกผัน อนุพันธ์ อินทิกรัล การขยายอนุกรมกำลัง และการแทนโดยใช้จำนวนเชิงซ้อน
คำนิยาม
ฟังก์ชันเลขชี้กำลังเป็นลักษณะทั่วไปของผลิตภัณฑ์ของจำนวน n เท่ากับ:
ย (n) = n = a·a·a···a,
ถึงเซตของจำนวนจริง x:
ย (x) = ก.
โดยที่ a เป็นจำนวนจริงคงที่ ซึ่งเรียกว่า พื้นฐานของฟังก์ชันเลขชี้กำลัง.
ฟังก์ชันเลขชี้กำลังที่มีฐาน a ก็เรียกอีกอย่างหนึ่งว่า เลขชี้กำลังของฐาน a.
ลักษณะทั่วไปดำเนินการดังนี้
สำหรับธรรมชาติ x = 1, 2, 3,...
ฟังก์ชันเลขชี้กำลังคือผลคูณของตัวประกอบ x:
.
นอกจากนี้ยังมีคุณสมบัติ (1.5-8) () ซึ่งเป็นไปตามกฎการคูณตัวเลข สำหรับค่าศูนย์และค่าลบของจำนวนเต็ม ฟังก์ชันเลขชี้กำลังถูกกำหนดโดยใช้สูตร (1.9-10) สำหรับค่าเศษส่วน x = m/n จำนวนตรรกยะ จะถูกกำหนดโดยสูตร (1.11) สำหรับค่าจริง ฟังก์ชันเลขชี้กำลังถูกกำหนดให้เป็นขีดจำกัดของลำดับ:
,
โดยที่ลำดับของจำนวนตรรกยะมาบรรจบกันเป็น x:
ด้วยคำจำกัดความนี้ ฟังก์ชันเอกซ์โพเนนเชียลถูกกำหนดไว้สำหรับ all และเป็นไปตามคุณสมบัติ (1.5-8) เช่นเดียวกับค่า x ตามธรรมชาติ
สูตรทางคณิตศาสตร์ที่เข้มงวดของคำจำกัดความของฟังก์ชันเอ็กซ์โปเนนเชียลและการพิสูจน์คุณสมบัติของฟังก์ชันมีให้ในหน้า “คำจำกัดความและการพิสูจน์คุณสมบัติของฟังก์ชันเอ็กซ์โปเนนเชียล”
คุณสมบัติของฟังก์ชันเลขชี้กำลัง
ฟังก์ชันเลขชี้กำลัง y = a x มีคุณสมบัติต่อไปนี้บนเซตของจำนวนจริง ():
(1.1)
กำหนดและต่อเนื่อง สำหรับ , สำหรับทั้งหมด ;
(1.2)
สำหรับ ≠ 1
มีหลายความหมาย
(1.3)
เพิ่มขึ้นอย่างเคร่งครัดที่ , ลดลงอย่างเคร่งครัดที่ ,
คงที่ที่ ;
(1.4)
ที่ ;
ที่ ;
(1.5)
;
(1.6)
;
(1.7)
;
(1.8)
;
(1.9)
;
(1.10)
;
(1.11)
,
.
สูตรที่มีประโยชน์อื่นๆ
.
สูตรการแปลงเป็นฟังก์ชันเลขชี้กำลังที่มีฐานเลขชี้กำลังต่างกัน:
เมื่อ b = e เราได้นิพจน์ของฟังก์ชันเลขชี้กำลังผ่านเลขชี้กำลัง:
ค่านิยมส่วนตัว
, , , , .
 รูปนี้แสดงกราฟของฟังก์ชันเลขชี้กำลัง
รูปนี้แสดงกราฟของฟังก์ชันเลขชี้กำลัง
ย (x) = ก
สำหรับสี่ค่า ฐานระดับ:ก= 2
, ก = 8
, ก = 1/2
และ ก = 1/8
. จะเห็นได้ว่าสำหรับ > 1
ฟังก์ชันเอ็กซ์โปเนนเชียลจะเพิ่มขึ้นแบบซ้ำซากจำเจ ยิ่งฐานของระดับ a มีขนาดใหญ่เท่าใด การเติบโตก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น ที่ 0
< a < 1
ฟังก์ชันเอกซ์โปเนนเชียลจะลดลงแบบซ้ำซากจำเจ ยิ่งเลขชี้กำลัง a น้อย ค่าการลดลงก็จะยิ่งมากขึ้นเท่านั้น
จากน้อยไปมากจากมากไปน้อย
ฟังก์ชันเอ็กซ์โปเนนเชียลสำหรับเป็นแบบโมโนโทนิกอย่างเคร่งครัด ดังนั้นจึงไม่มีเอ็กซ์ตรีม คุณสมบัติหลักแสดงไว้ในตาราง
| y = a x , a > 1 | y = ขวาน 0 < a < 1 | |
| โดเมน | - ∞ < x < + ∞ | - ∞ < x < + ∞ |
| ช่วงของค่า | 0 < y < + ∞ | 0 < y < + ∞ |
| โมโนโทน | เพิ่มขึ้นอย่างน่าเบื่อ | ลดลงอย่างน่าเบื่อ |
| ศูนย์, y = 0 | เลขที่ | เลขที่ |
| จุดตัดกับแกนพิกัด x = 0 | ย = 1 | ย = 1 |
| + ∞ | 0 | |
| 0 | + ∞ |
ฟังก์ชันผกผัน
ค่าผกผันของฟังก์ชันเลขชี้กำลังที่มีฐาน a คือลอการิทึมของฐาน a
ถ้าอย่างนั้น
.
ถ้าอย่างนั้น
.
การหาความแตกต่างของฟังก์ชันเลขชี้กำลัง
หากต้องการแยกความแตกต่างของฟังก์ชันเอ็กซ์โปเนนเชียล ฐานจะต้องลดลงเหลือจำนวน e ใช้ตารางอนุพันธ์และกฎการหาอนุพันธ์ ฟังก์ชั่นที่ซับซ้อน.
ในการทำเช่นนี้ คุณต้องใช้คุณสมบัติของลอการิทึม
และสูตรจากตารางอนุพันธ์คือ
.
ให้ฟังก์ชันเลขชี้กำลังได้รับ:
.
เรานำมันไปที่ฐาน e:
ลองใช้กฎการหาอนุพันธ์ของฟังก์ชันที่ซับซ้อนกันดีกว่า เมื่อต้องการทำเช่นนี้ ให้แนะนำตัวแปร
แล้ว
จากตารางอนุพันธ์ที่เรามี (แทนที่ตัวแปร x ด้วย z):
.
เนื่องจากเป็นค่าคงที่ อนุพันธ์ของ z เทียบกับ x จะเท่ากับ
.
ตามกฎการหาอนุพันธ์ของฟังก์ชันเชิงซ้อน:
.
อนุพันธ์ของฟังก์ชันเลขชี้กำลัง
.
อนุพันธ์ของลำดับที่ n:
.
การหาสูตร > > >
ตัวอย่างการสร้างความแตกต่างของฟังก์ชันเลขชี้กำลัง
ค้นหาอนุพันธ์ของฟังก์ชัน
ย = 3 5 x
สารละลาย
ลองแสดงฐานของฟังก์ชันเอ็กซ์โปเนนเชียลผ่านตัวเลข e กัน
3 = อี อิน 3
แล้ว
.
ป้อนตัวแปร
.
แล้ว
จากตารางอนุพันธ์เราพบว่า:
.
เพราะว่า 5อิน3เป็นค่าคงที่ ดังนั้นอนุพันธ์ของ z เทียบกับ x จะเท่ากับ:
.
ตามกฎการหาอนุพันธ์ของฟังก์ชันที่ซับซ้อน เราจะได้:
.
คำตอบ
บูรณาการ
นิพจน์ที่ใช้จำนวนเชิงซ้อน
พิจารณาฟังก์ชันจำนวนเชิงซ้อน z:
ฉ (z) = ก
โดยที่ z = x + iy; ฉัน 2 = - 1
.
ให้เราแสดงค่าคงที่เชิงซ้อน a ในรูปของโมดูลัส r และอาร์กิวเมนต์ φ:
a = r e ฉัน φ
แล้ว
.
อาร์กิวเมนต์ φ ไม่ได้ถูกกำหนดไว้โดยเฉพาะ ใน ปริทัศน์
φ = φ 0 + 2 πn,
โดยที่ n คือจำนวนเต็ม ดังนั้นฟังก์ชัน f (ซ)ยังไม่ชัดเจน ความสำคัญหลักมักได้รับการพิจารณา
.
การขยายซีรีส์
.
อ้างอิง:
ใน. บรอนสไตน์, เค.เอ. Semendyaev คู่มือคณิตศาสตร์สำหรับวิศวกรและนักศึกษา "Lan", 2552
นำเสนอคุณสมบัติและกราฟของฟังก์ชันกำลังสำหรับค่าต่างๆ ของเลขชี้กำลัง สูตรพื้นฐาน ขอบเขตของคำนิยามและเซตของค่า ความเท่าเทียมกัน ความซ้ำซ้อน การเพิ่มขึ้นและการลดลง สุดขั้ว ความนูน การผันจุด จุดตัดกับแกนพิกัด ขีดจำกัด ค่าเฉพาะ
สูตรที่มีฟังก์ชันยกกำลัง
ในโดเมนของคำจำกัดความของฟังก์ชันกำลัง y = x p สูตรต่อไปนี้ถือเป็น:
;
;
;
;
;
;
;
;
.
คุณสมบัติของฟังก์ชันกำลังและกราฟ
ฟังก์ชันยกกำลังที่มีเลขชี้กำลังเท่ากับศูนย์, p = 0
หากเลขชี้กำลังของฟังก์ชันกำลัง y = x p เท่ากับศูนย์, p = 0 ดังนั้นฟังก์ชันกำลังจะถูกกำหนดสำหรับ x ≠ 0 ทั้งหมดและเป็นค่าคงที่เท่ากับ 1:
y = x พี = x 0 = 1, x ≠ 0
ฟังก์ชันยกกำลังที่มีเลขชี้กำลังคี่ธรรมชาติ, p = n = 1, 3, 5, ...
พิจารณาฟังก์ชันยกกำลัง y = x p = xn โดยมีเลขชี้กำลังคี่ธรรมชาติ n = 1, 3, 5, ... ตัวบ่งชี้นี้สามารถเขียนได้ในรูปแบบ: n = 2k + 1 โดยที่ k = 0, 1, 2, 3, ... เป็นจำนวนเต็มที่ไม่เป็นลบ ด้านล่างนี้คือคุณสมบัติและกราฟของฟังก์ชันดังกล่าว

กราฟของฟังก์ชันกำลัง y = x n พร้อมเลขชี้กำลังคี่ตามธรรมชาติสำหรับค่าต่างๆ ของเลขชี้กำลัง n = 1, 3, 5, ....
โดเมน: -∞ < x < ∞
ความหมายหลายประการ: -∞ < y < ∞
ความเท่าเทียมกัน:แปลก y(-x) = - y(x)
โมโนโทน:เพิ่มขึ้นอย่างน่าเบื่อ
สุดขั้ว:เลขที่
นูน:
ที่-∞< x < 0
выпукла вверх
เวลา 0< x < ∞
выпукла вниз
จุดเปลี่ยน: x = 0, y = 0
x = 0, y = 0
ขีดจำกัด:
;
ค่าส่วนตัว:
ที่ x = -1,
y(-1) = (-1) n ≡ (-1) 2k+1 = -1
ที่ x = 0, y(0) = 0 n = 0
สำหรับ x = 1, y(1) = 1 n = 1
ฟังก์ชั่นย้อนกลับ:
สำหรับ n = 1 ฟังก์ชันจะกลับกัน: x = y
สำหรับ n ≠ 1 ฟังก์ชันผกผันคือรากของระดับ n:
ฟังก์ชันยกกำลังที่มีเลขชี้กำลังคู่ตามธรรมชาติ p = n = 2, 4, 6, ...
พิจารณาฟังก์ชันยกกำลัง y = x p = xn โดยมีเลขชี้กำลังเลขคู่ธรรมชาติ n = 2, 4, 6, ... ตัวบ่งชี้นี้สามารถเขียนในรูปแบบ: n = 2k โดยที่ k = 1, 2, 3, ... - โดยธรรมชาติ คุณสมบัติและกราฟของฟังก์ชันดังกล่าวมีดังต่อไปนี้

กราฟของฟังก์ชันยกกำลัง y = x n พร้อมเลขชี้กำลังคู่แบบธรรมชาติสำหรับค่าต่างๆ ของเลขชี้กำลัง n = 2, 4, 6, ....
โดเมน: -∞ < x < ∞
ความหมายหลายประการ: 0 ≤ ย< ∞
ความเท่าเทียมกัน:เท่ากัน y(-x) = y(x)
โมโนโทน:
สำหรับ x ≤ 0 ลดลงอย่างน่าเบื่อ
สำหรับ x ≥ 0 เพิ่มขึ้นอย่างน่าเบื่อ
สุดขั้ว:ขั้นต่ำ x = 0, y = 0
นูน:นูนลง
จุดเปลี่ยน:เลขที่
จุดตัดกับแกนพิกัด: x = 0, y = 0
ขีดจำกัด:
;
ค่าส่วนตัว:
ที่ x = -1, y(-1) = (-1) n ≡ (-1) 2k = 1
ที่ x = 0, y(0) = 0 n = 0
สำหรับ x = 1, y(1) = 1 n = 1
ฟังก์ชั่นย้อนกลับ:
สำหรับ n = 2, รากที่สอง:
สำหรับ n ≠ 2 รากของระดับ n:
ฟังก์ชันยกกำลังที่มีเลขชี้กำลังจำนวนเต็มลบ, p = n = -1, -2, -3, ...
พิจารณาฟังก์ชันยกกำลัง y = x p = xn ด้วยจำนวนเต็ม ตัวบ่งชี้เชิงลบองศา n = -1, -2, -3, ... . หากเราใส่ n = -k โดยที่ k = 1, 2, 3, ... เป็นจำนวนธรรมชาติ จากนั้นจะสามารถแสดงเป็น:

กราฟของฟังก์ชันกำลัง y = x n พร้อมเลขชี้กำลังจำนวนเต็มลบสำหรับค่าต่างๆ ของเลขชี้กำลัง n = -1, -2, -3, ... .
เลขชี้กำลังคี่ n = -1, -3, -5, ...
ด้านล่างนี้คือคุณสมบัติของฟังก์ชัน y = xn ที่มีเลขชี้กำลังลบคี่ n = -1, -3, -5, ....
โดเมน: x ≠ 0
ความหมายหลายประการ:ใช่ ≠ 0
ความเท่าเทียมกัน:แปลก y(-x) = - y(x)
โมโนโทน:ลดลงอย่างน่าเบื่อ
สุดขั้ว:เลขที่
นูน:
ที่ x< 0
:
выпукла вверх
สำหรับ x > 0: นูนลง
จุดเปลี่ยน:เลขที่
จุดตัดกับแกนพิกัด:เลขที่
เข้าสู่ระบบ:
ที่ x< 0, y < 0
สำหรับ x > 0, y > 0
ขีดจำกัด:
; ; ;
ค่าส่วนตัว:
สำหรับ x = 1, y(1) = 1 n = 1
ฟังก์ชั่นย้อนกลับ:
เมื่อ n = -1,
ที่ n< -2
,
เลขยกกำลังคู่ n = -2, -4, -6, ...
ด้านล่างนี้คือคุณสมบัติของฟังก์ชัน y = xn ที่มีเลขชี้กำลังเป็นลบคู่ n = -2, -4, -6, ....
โดเมน: x ≠ 0
ความหมายหลายประการ:ใช่ > 0
ความเท่าเทียมกัน:เท่ากัน y(-x) = y(x)
โมโนโทน:
ที่ x< 0
:
монотонно возрастает
สำหรับ x > 0: ลดลงอย่างน่าเบื่อ
สุดขั้ว:เลขที่
นูน:นูนลง
จุดเปลี่ยน:เลขที่
จุดตัดกับแกนพิกัด:เลขที่
เข้าสู่ระบบ:ใช่ > 0
ขีดจำกัด:
; ; ;
ค่าส่วนตัว:
สำหรับ x = 1, y(1) = 1 n = 1
ฟังก์ชั่นย้อนกลับ:
ที่ n = -2,
ที่ n< -2
,
ฟังก์ชันยกกำลังพร้อมเลขชี้กำลังที่เป็นตรรกยะ (เศษส่วน)
พิจารณาฟังก์ชันยกกำลัง y = x p ที่มีเลขชี้กำลังที่เป็นตรรกยะ (เศษส่วน) โดยที่ n เป็นจำนวนเต็ม m > 1 เป็นจำนวนธรรมชาติ ยิ่งกว่านั้น n, m ไม่มีตัวหารร่วม
ตัวส่วนของตัวบ่งชี้เศษส่วนเป็นเลขคี่
ให้ตัวส่วนของเลขชี้กำลังเศษส่วนเป็นเลขคี่: m = 3, 5, 7, ... . ในกรณีนี้ฟังก์ชันกำลัง x p ถูกกำหนดไว้สำหรับทั้งค่าบวกและค่าลบของอาร์กิวเมนต์ x ลองพิจารณาคุณสมบัติของฟังก์ชันยกกำลังดังกล่าวเมื่อเลขชี้กำลัง p อยู่ภายในขีดจำกัดที่กำหนด
ค่า p เป็นลบ p< 0
ให้เลขชี้กำลังตรรกยะ (ที่มีตัวหารคี่ m = 3, 5, 7, ...) น้อยกว่าศูนย์:

กราฟของฟังก์ชันกำลังที่มีเลขชี้กำลังลบตรรกยะสำหรับค่าต่างๆ ของเลขชี้กำลัง โดยที่ m = 3, 5, 7, ... - คี่
ตัวเศษคี่, n = -1, -3, -5, ...
เรานำเสนอคุณสมบัติของฟังก์ชันยกกำลัง y = x p ด้วยเลขชี้กำลังลบตรรกยะ โดยที่ n = -1, -3, -5, ... เป็นจำนวนเต็มลบคี่ m = 3, 5, 7 ... คือ จำนวนเต็มธรรมชาติคี่
โดเมน: x ≠ 0
ความหมายหลายประการ:ใช่ ≠ 0
ความเท่าเทียมกัน:แปลก y(-x) = - y(x)
โมโนโทน:ลดลงอย่างน่าเบื่อ
สุดขั้ว:เลขที่
นูน:
ที่ x< 0
:
выпукла вверх
สำหรับ x > 0: นูนลง
จุดเปลี่ยน:เลขที่
จุดตัดกับแกนพิกัด:เลขที่
เข้าสู่ระบบ:
ที่ x< 0, y < 0
สำหรับ x > 0, y > 0
ขีดจำกัด:
; ; ;
ค่าส่วนตัว:
ที่ x = -1, y(-1) = (-1) n = -1
สำหรับ x = 1, y(1) = 1 n = 1
ฟังก์ชั่นย้อนกลับ:
ตัวเศษเลขคู่ n = -2, -4, -6, ...
คุณสมบัติของฟังก์ชันกำลัง y = x p ที่มีเลขชี้กำลังลบตรรกยะ โดยที่ n = -2, -4, -6, ... เป็นจำนวนเต็มลบคู่ m = 3, 5, 7 ... เป็นจำนวนเต็มธรรมชาติคี่ .
โดเมน: x ≠ 0
ความหมายหลายประการ:ใช่ > 0
ความเท่าเทียมกัน:เท่ากัน y(-x) = y(x)
โมโนโทน:
ที่ x< 0
:
монотонно возрастает
สำหรับ x > 0: ลดลงอย่างน่าเบื่อ
สุดขั้ว:เลขที่
นูน:นูนลง
จุดเปลี่ยน:เลขที่
จุดตัดกับแกนพิกัด:เลขที่
เข้าสู่ระบบ:ใช่ > 0
ขีดจำกัด:
; ; ;
ค่าส่วนตัว:
ที่ x = -1, y(-1) = (-1) n = 1
สำหรับ x = 1, y(1) = 1 n = 1
ฟังก์ชั่นย้อนกลับ:
ค่า p เป็นค่าบวก น้อยกว่าหนึ่ง 0< p < 1

กราฟของฟังก์ชันยกกำลังที่มีเลขชี้กำลังตรรกยะ (0< p < 1 ) при различных значениях показателя степени , где m = 3, 5, 7, ... - нечетное.
ตัวเศษคี่, n = 1, 3, 5, ...
< p < 1 , где n = 1, 3, 5, ... - нечетное натуральное, m = 3, 5, 7 ... - нечетное натуральное.
โดเมน: -∞ < x < +∞
ความหมายหลายประการ: -∞ < y < +∞
ความเท่าเทียมกัน:แปลก y(-x) = - y(x)
โมโนโทน:เพิ่มขึ้นอย่างน่าเบื่อ
สุดขั้ว:เลขที่
นูน:
ที่ x< 0
:
выпукла вниз
สำหรับ x > 0: นูนขึ้น
จุดเปลี่ยน: x = 0, y = 0
จุดตัดกับแกนพิกัด: x = 0, y = 0
เข้าสู่ระบบ:
ที่ x< 0, y < 0
สำหรับ x > 0, y > 0
ขีดจำกัด:
;
ค่าส่วนตัว:
ที่ x = -1, y(-1) = -1
ที่ x = 0, y(0) = 0
สำหรับ x = 1, y(1) = 1
ฟังก์ชั่นย้อนกลับ:
ตัวเศษ, n = 2, 4, 6, ...
คุณสมบัติของฟังก์ชันยกกำลัง y = x p ที่มีเลขชี้กำลังเชิงตรรกยะภายใน 0 จะถูกนำเสนอ< p < 1 , где n = 2, 4, 6, ... - четное натуральное, m = 3, 5, 7 ... - нечетное натуральное.
โดเมน: -∞ < x < +∞
ความหมายหลายประการ: 0 ≤ ย< +∞
ความเท่าเทียมกัน:เท่ากัน y(-x) = y(x)
โมโนโทน:
ที่ x< 0
:
монотонно убывает
สำหรับ x > 0: เพิ่มขึ้นอย่างซ้ำซากจำเจ
สุดขั้ว:ขั้นต่ำที่ x = 0, y = 0
นูน:นูนขึ้นด้านบนสำหรับ x ≠ 0
จุดเปลี่ยน:เลขที่
จุดตัดกับแกนพิกัด: x = 0, y = 0
เข้าสู่ระบบ:สำหรับ x ≠ 0, y > 0
ขีดจำกัด:
;
ค่าส่วนตัว:
ที่ x = -1, y(-1) = 1
ที่ x = 0, y(0) = 0
สำหรับ x = 1, y(1) = 1
ฟังก์ชั่นย้อนกลับ:
ดัชนี p มากกว่าหนึ่ง p > 1

กราฟของฟังก์ชันยกกำลังพร้อมเลขชี้กำลังตรรกยะ (p > 1) สำหรับค่าต่างๆ ของเลขชี้กำลัง โดยที่ m = 3, 5, 7, ... - คี่
ตัวเศษคี่, n = 5, 7, 9, ...
คุณสมบัติของฟังก์ชันยกกำลัง y = x p โดยมีเลขชี้กำลังเชิงตรรกศาสตร์มากกว่าหนึ่ง: โดยที่ n = 5, 7, 9, ... - คี่โดยธรรมชาติ, m = 3, 5, 7 ... - คี่โดยธรรมชาติ
โดเมน: -∞ < x < ∞
ความหมายหลายประการ: -∞ < y < ∞
ความเท่าเทียมกัน:แปลก y(-x) = - y(x)
โมโนโทน:เพิ่มขึ้นอย่างน่าเบื่อ
สุดขั้ว:เลขที่
นูน:
ที่-∞< x < 0
выпукла вверх
เวลา 0< x < ∞
выпукла вниз
จุดเปลี่ยน: x = 0, y = 0
จุดตัดกับแกนพิกัด: x = 0, y = 0
ขีดจำกัด:
;
ค่าส่วนตัว:
ที่ x = -1, y(-1) = -1
ที่ x = 0, y(0) = 0
สำหรับ x = 1, y(1) = 1
ฟังก์ชั่นย้อนกลับ:
ตัวเศษ, n = 4, 6, 8, ...
คุณสมบัติของฟังก์ชันยกกำลัง y = x p โดยมีเลขชี้กำลังเชิงตรรกศาสตร์มากกว่าหนึ่ง: โดยที่ n = 4, 6, 8, ... - เป็นธรรมชาติ, m = 3, 5, 7 ... - เป็นธรรมชาติแปลก ๆ
โดเมน: -∞ < x < ∞
ความหมายหลายประการ: 0 ≤ ย< ∞
ความเท่าเทียมกัน:เท่ากัน y(-x) = y(x)
โมโนโทน:
ที่ x< 0
монотонно убывает
สำหรับ x > 0 เพิ่มขึ้นอย่างซ้ำซากจำเจ
สุดขั้ว:ขั้นต่ำที่ x = 0, y = 0
นูน:นูนลง
จุดเปลี่ยน:เลขที่
จุดตัดกับแกนพิกัด: x = 0, y = 0
ขีดจำกัด:
;
ค่าส่วนตัว:
ที่ x = -1, y(-1) = 1
ที่ x = 0, y(0) = 0
สำหรับ x = 1, y(1) = 1
ฟังก์ชั่นย้อนกลับ:
ตัวส่วนของตัวบ่งชี้เศษส่วนคือเลขคู่
ให้ตัวส่วนของเลขชี้กำลังเศษส่วนเป็นเลขคู่: m = 2, 4, 6, ... . ในกรณีนี้ไม่ได้กำหนดฟังก์ชันกำลัง x p สำหรับค่าลบของอาร์กิวเมนต์ คุณสมบัติของมันตรงกับคุณสมบัติของฟังก์ชันกำลังที่มีเลขชี้กำลังไม่ลงตัว (ดูหัวข้อถัดไป)
ฟังก์ชันยกกำลังที่มีเลขชี้กำลังไม่ลงตัว
พิจารณาฟังก์ชันยกกำลัง y = x p พร้อมด้วยเลขชี้กำลังที่ไม่ลงตัว p คุณสมบัติของฟังก์ชันดังกล่าวแตกต่างจากที่กล่าวไว้ข้างต้นเนื่องจากไม่ได้กำหนดไว้สำหรับค่าลบของอาร์กิวเมนต์ x สำหรับค่าบวกของอาร์กิวเมนต์ คุณสมบัติจะขึ้นอยู่กับค่าของเลขชี้กำลัง p เท่านั้น และไม่ได้ขึ้นอยู่กับว่า p เป็นจำนวนเต็ม ตรรกยะ หรืออตรรกยะ
y = x p สำหรับค่าต่าง ๆ ของเลขชี้กำลัง p
ฟังก์ชันยกกำลังที่มีเลขชี้กำลังเป็นลบ p< 0
โดเมน: x > 0
ความหมายหลายประการ:ใช่ > 0
โมโนโทน:ลดลงอย่างน่าเบื่อ
นูน:นูนลง
จุดเปลี่ยน:เลขที่
จุดตัดกับแกนพิกัด:เลขที่
ขีดจำกัด: ;
ความหมายส่วนตัว:สำหรับ x = 1, y(1) = 1 p = 1
ฟังก์ชันกำลังที่มีเลขชี้กำลังบวก p > 0
ตัวบ่งชี้น้อยกว่าหนึ่ง 0< p < 1
โดเมน: x ≥ 0
ความหมายหลายประการ:ใช่ ≥ 0
โมโนโทน:เพิ่มขึ้นอย่างน่าเบื่อ
นูน:นูนขึ้น
จุดเปลี่ยน:เลขที่
จุดตัดกับแกนพิกัด: x = 0, y = 0
ขีดจำกัด:
ค่าส่วนตัว:สำหรับ x = 0, y(0) = 0 p = 0
สำหรับ x = 1, y(1) = 1 p = 1
ตัวบ่งชี้มีค่ามากกว่าหนึ่ง p > 1
โดเมน: x ≥ 0
ความหมายหลายประการ:ใช่ ≥ 0
โมโนโทน:เพิ่มขึ้นอย่างน่าเบื่อ
นูน:นูนลง
จุดเปลี่ยน:เลขที่
จุดตัดกับแกนพิกัด: x = 0, y = 0
ขีดจำกัด:
ค่าส่วนตัว:สำหรับ x = 0, y(0) = 0 p = 0
สำหรับ x = 1, y(1) = 1 p = 1
อ้างอิง:
ใน. บรอนสไตน์, เค.เอ. Semendyaev คู่มือคณิตศาสตร์สำหรับวิศวกรและนักศึกษา "Lan", 2552

